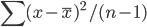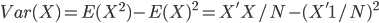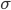This is a post I wrote on company's internal wiki... just want a backup here.
Three points to bear in mind:
- Outliers are not bad; they just behave differently.
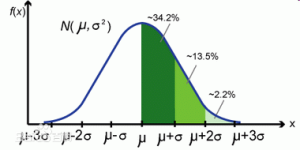
- Many statistics are sensitive to outliers. e.g. the mean and every model that relies on the mean.
- Abnormal detection is another topic; this post focus on exploring robust models.
Make the analysis robust to outliers:
|
Method
|
Action
|
Advantage
|
Concern
|
|---|---|---|---|
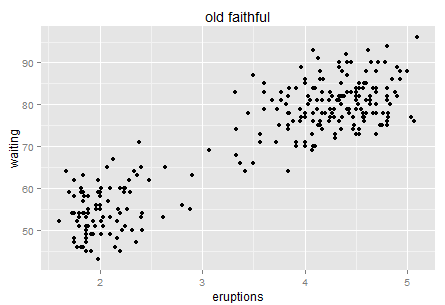
| Remove the outliers | remove outliers according to a certain threshold or calculation (perhaps via unsupervised models); only focus on the left subsample. | In most cases the signal will be more clear from concentrated subsample. | Hard to generalize the effect to entire population; hard to define a threshold. |
| Capping the outliers | cap the outliers to a certain value. | All observations are kept so easy to map the effect to all samples afterward; outliers' impacts are punished. | softer compared to removing the outliers; hard to find the threshold or capping rule. |
| Control for covariates | include some control variables in the regression. some how analyze the "difference" but not just linear and constant difference. | Introduce some relevant factors to gain a precise estimation and better learning. | Need to find the right control variable. Irrelevant covariates will only introduce noise. |
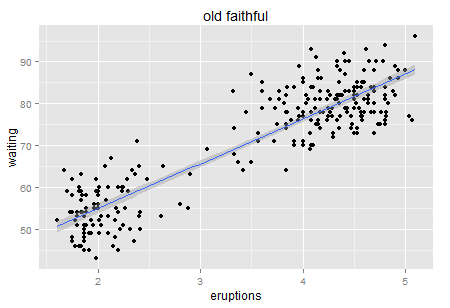
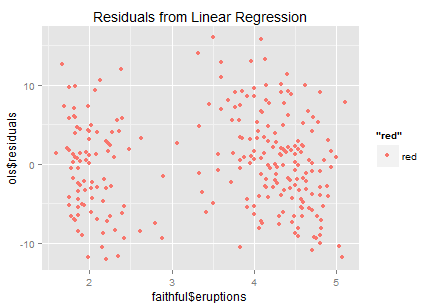
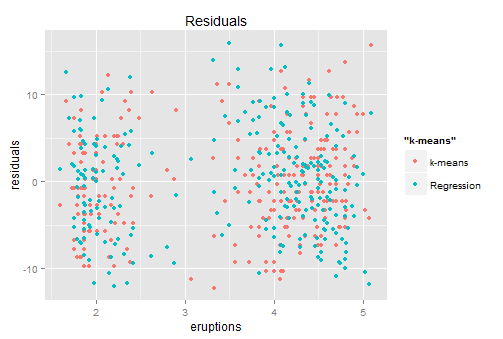
| Regression to the median | Median is more robust than the mean when outliers persist. Run a full quantile regression if possible; or just 50% quantile which is the median regression. | Get a clear directional signal; robust to outliers so no need to choose any threshold. | Hard to generalize the treatment effect to all population. |
| Quantile Regression | Generalized model from above; help you understand subtle difference in each quantile. | Gain more knowledge on the distribution rather than single point and great explanation power. | Computational expensive; hard for further generalization; |
| Subsample Regression | Instead of regress to each quantile, a subsample regression only run regression within each strata of the whole sample (say, sub-regression in each decile). | Identical to introducing a categorical variable for each decile in regression; also help inspect each subsample. | only directional; higher accumulated false-positive rate. |
| Take log() or other numerical transformations | It's a numerical trick that shrink the range to a narrower one (high punishment on the high values). | Easy to compute and map back to the real value; get directional results. | May not be enough to obtain a clear signal. |
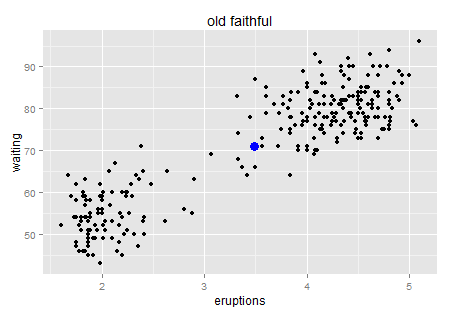
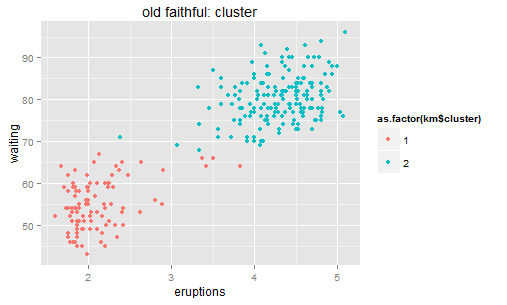
| Unsupervised study for higher dimensions | This is more about outlier detection. When there are more than one dimension to define an outlier, some unsupervised models like K-means would help (identify the distance to the center). | deals with higher dimensions | exploration only.
|
| Rank based methods | Measure ranks of outcome variables instead of the absolute value. | immunized to outliers. | Hard to generalize the treatment effect to all population.
|
That's all I could think of for now...any addition is welcome 🙂
------- update on Apr 8, 2016 --------
Some new notes:
- "outliers" may not be the right name for heavy tails.
- Rank methods.