As far as I know, there are several ways to solve a linear regression with computers. Here is a summary.
- Native close form solution: just
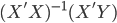 . We can always solve that inverse matrix. It works fine for small dataset but to inverse a large matrix might be very computations expensive.
. We can always solve that inverse matrix. It works fine for small dataset but to inverse a large matrix might be very computations expensive. - QR decomposition: this is the default method in R when you run lm(). In short, QR decomposition is to decompose the X matrix to X = QR where Q is an orthogonal matrix and R is an upper triangular matrix. Therefore,
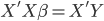 and then
and then 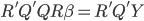 then
then 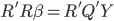 then
then 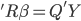 . Because R is a upper triangular matrix then we can get beta directly after computing Q'Y. (More details)
. Because R is a upper triangular matrix then we can get beta directly after computing Q'Y. (More details) - Regression anatomy formula: my boss mentioned it (thanks man! I never notice that) and I read the book Mostly Harmless Econometrics again today, on page 36 footnote, there is the regression anatomy formula. Basically if you have solved a regression already and just want to add an additional control variable, then you can follow this approach to make the computation easy.

Especially if you have already computed a simple A/B test (i.e. only one dummy variable on the right hand side), then you can obtain such residues directly without running a real regression and then compute the estimate for your additional control variables straightforwardly. The variance estimate also follows. - Bootstrap: in most case bootstrap is expensive because you need to re-draw repeatably from your sample. However, if it is a very large data and it is naturally distribution over a parallel file distribution system (e.g. Hadoop), then draw from each node could be the best map-reduce strategy you may adopt in this case. As far as I know, the rHadoop package accommodates such idea for their parallel lm() function (or map-reduce algorithm).
Any other ways?




